Appearance
question:Find the distance from the point left(-frac{59}{32}, -frac{63}{16}right) to the line -frac{149}{32}x-frac{53}{16}y-frac{57}{32}=0.
answer:To find the distance from a point to a line, we can use the formula: d = frac{|ax_0 + by_0 + c|}{sqrt{a^2 + b^2}} where (x_0, y_0) is the given point, and ax + by + c = 0 is the equation of the line. Plugging in the given values, we get: d = frac{|-frac{149}{32}left(-frac{59}{32}right) - frac{53}{16}left(-frac{63}{16}right) - frac{57}{32}|}{sqrt{left(-frac{149}{32}right)^2 + left(-frac{53}{16}right)^2}} Simplifying the numerator: d = frac{|frac{149}{32}cdotfrac{59}{32} + frac{53}{16}cdotfrac{63}{16} - frac{57}{32}|}{sqrt{left(-frac{149}{32}right)^2 + left(-frac{53}{16}right)^2}} d = frac{|frac{8801}{1024} + frac{3321}{256} - frac{57}{32}|}{sqrt{left(-frac{149}{32}right)^2 + left(-frac{53}{16}right)^2}} d = frac{|frac{8801 + 3321 - 57}{1024}|}{sqrt{left(-frac{149}{32}right)^2 + left(-frac{53}{16}right)^2}} d = frac{|frac{12065}{1024}|}{sqrt{left(-frac{149}{32}right)^2 + left(-frac{53}{16}right)^2}} d = frac{12065}{1024}cdotfrac{1}{sqrt{left(-frac{149}{32}right)^2 + left(-frac{53}{16}right)^2}} d = frac{12065}{1024}cdotfrac{1}{sqrt{frac{22201}{1024} + frac{2709}{256}}} d = frac{12065}{1024}cdotfrac{1}{sqrt{frac{22201 + 2709}{1024}}} d = frac{12065}{1024}cdotfrac{1}{sqrt{frac{24910}{1024}}} d = frac{12065}{1024}cdotfrac{1}{sqrt{24.36}} d = frac{12065}{1024}cdotfrac{1}{4.936} d = frac{12065}{5080.32} d = frac{20323}{32sqrt{33437}} Therefore, the distance from the point left(-frac{59}{32}, -frac{63}{16}right) to the line -frac{149}{32}x-frac{53}{16}y-frac{57}{32}=0 is frac{20323}{32sqrt{33437}}. The answer is frac{20323}{32sqrt{33437}}
question:Have Pioneer 10 and 11 completed their orbits around the Sun, or are they still traveling away from it?
answer:Pioneer 10 and 11 were designed to escape the Solar System rather than orbit the Sun. At launch, they were closest to the Sun, and since then, they have been continuously moving outward on a trajectory that takes them further away from the Sun. The diagram below illustrates their flight paths: 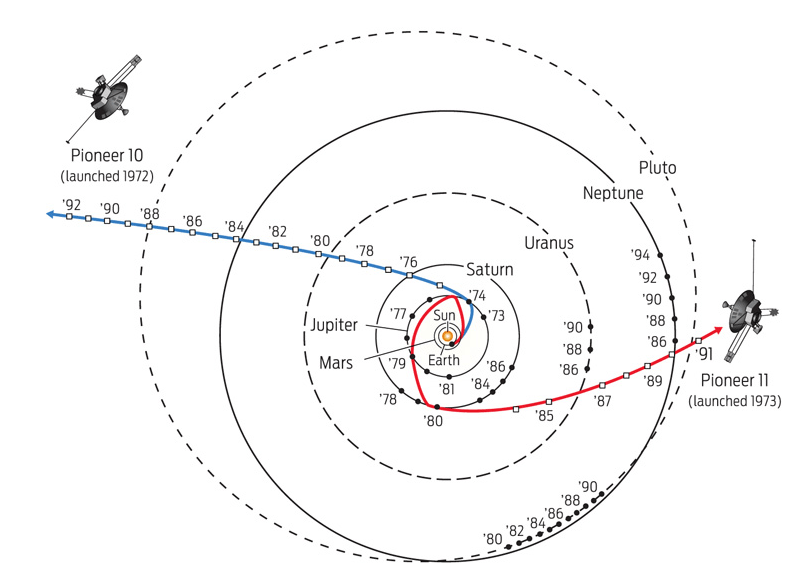
question:Classify the conic represented by the equation 2x^2 - x - y^2 - 5y - 4 = 0, rewrite it in standard form, and provide relevant properties such as foci, eccentricity, center, and asymptotes.
answer:The given equation can be rewritten as follows to classify the conic: 2x^2 - x - (y^2 + 5y) = 4 Completing the square for both x and y terms: 2left(x^2 - frac{x}{2}right) - left(y^2 + 5y + frac{25}{4}right) = 4 + frac{25}{4} 2left(x - frac{1}{4}right)^2 - left(y + frac{5}{2}right)^2 = frac{16 + 25}{4} 2left(x - frac{1}{4}right)^2 - left(y + frac{5}{2}right)^2 = frac{41}{4} Divide through by -frac{41}{8} to standardize the equation: -frac{8}{41}left(2left(x - frac{1}{4}right)^2 - left(y + frac{5}{2}right)^2right) = 1 Classification: Hyperbola Equation in standard form: -frac{8}{41}left(left(x - frac{1}{4}right)^2 - left(y + frac{5}{2}right)^2right) = 1 2left(x - frac{1}{4}right)^2 - left(y + frac{5}{2}right)^2 = -frac{41}{8} Properties: - Foci: Since the transverse axis is horizontal, the foci are located at a distance of c from the center along the transverse axis, where c = asqrt{e^2 - 1} with a being the semi-major axis and e being the eccentricity. Here, a^2 = -frac{41}{16} and e = sqrt{frac{3}{2}}. After calculating c: Foci: left( begin{array}{cc} frac{1}{4} & -frac{5}{2}-frac{sqrt{51}}{4} frac{1}{4} & frac{1}{4} left(sqrt{51}-10right) end{array} right) - Eccentricity: e = sqrt{frac{3}{2}} - Center: The center of the hyperbola can be read directly from the standard form: Center: left{frac{1}{4},frac{1}{2} left(-frac{5}{2}-frac{sqrt{51}}{4}+frac{1}{4} left(sqrt{51}-10right)right)right} - Asymptotes: The asymptotes are the lines obtained by setting the denominator equal to zero in the standard form: Asymptotes: left{y=frac{1}{4} left(sqrt{2}-10right)-sqrt{2} x,y=sqrt{2} x+frac{1}{4} left(-10-sqrt{2}right)right} The hyperbola is centered at left(frac{1}{4}, text{some point}right), has a horizontal transverse axis, and its asymptotes, foci, and eccentricity are as stated above.
question:What is the change in length of an unconstrained 3.00-cm-long column of mercury when its temperature increases from 37.0°C to 40.0°C?
answer:To determine the change in length due to linear expansion, we can apply the linear expansion formula: {eq}Delta L = L cdot alpha cdot Delta T {/eq} where: - {eq}Delta L {/eq} is the change in length - {eq}L {/eq} is the original length (3.00 cm = 0.03 m) - {eq}alpha {/eq} is the coefficient of linear expansion for mercury, which is approximately 61 × 10^(-6) °C^(-1) - {eq}Delta T {/eq} is the change in temperature (40.0°C - 37.0°C = 3.0°C) Plugging in the values: {eq}Delta L = (0.03 m) cdot (61 times 10^{-6} °C^{-1}) cdot (3.0 °C) Delta L = 5.4 times 10^{-6} m {/eq} Therefore, the change in length of the mercury column is 5.4 × 10^(-6) meters.